Activity Detection for Massive Random Access using Covariance Learning Matching Pursuit (CL-MP) method.
Also a demo simulation in the paper is provided.
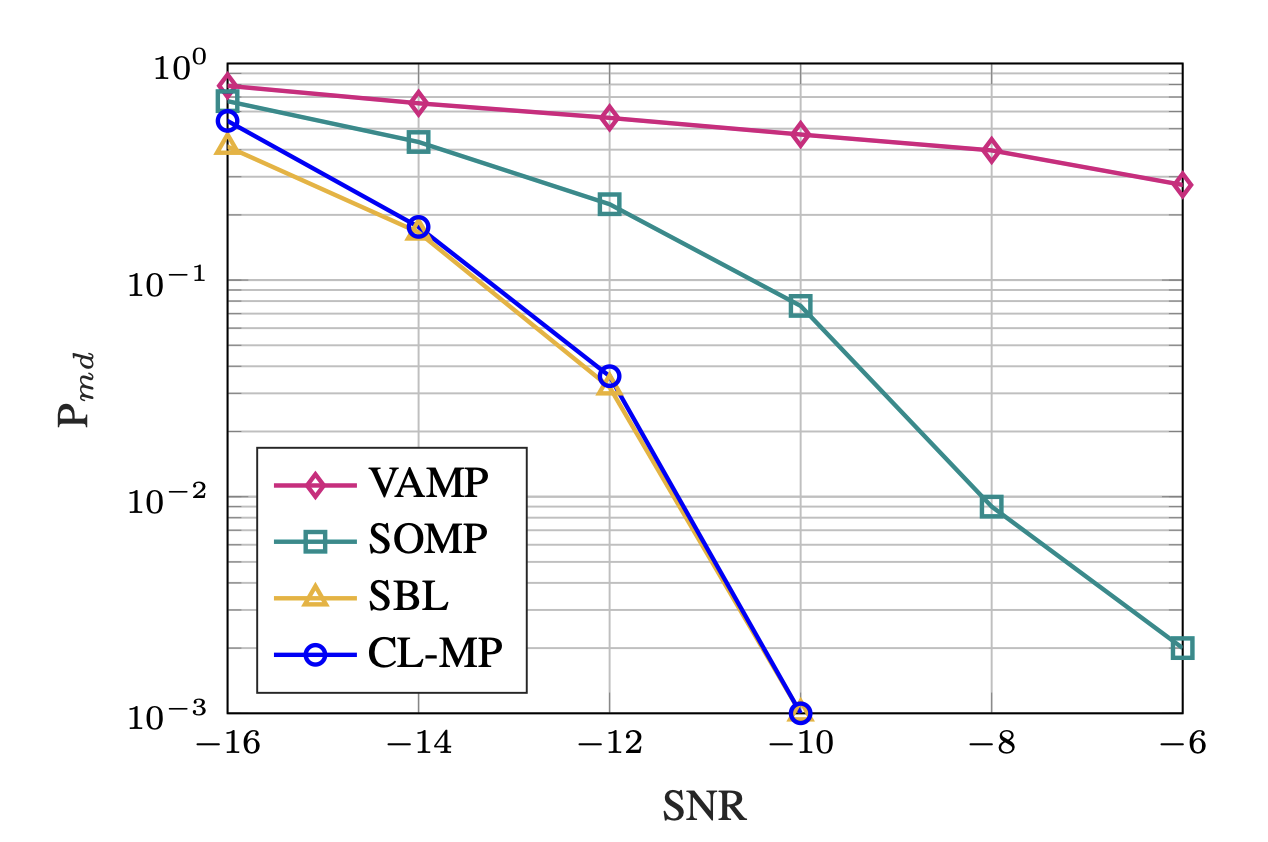For more information, see:
Activity Detection for Massive Random Access using Covariance-based Matching Pursuit, Leatile Marata, Esa Ollila, Hirley Alves, arXiv:2405.02741 [eess.SP]
[
Github]
Greedy Capon Beamformer
We provide an efficient function to compute the Greedy Capon Beamformer (GCB) which is a (sparse) greedy version of the standard Capon Beamformer (SCB). GCB is fast to compute, often outperforms SCB with a clear margin,
and unlike the SCB it is not affected by coherence of the signals. In the Github repo, we also include a demo example that can be used to reproduces Figures
in the paper.
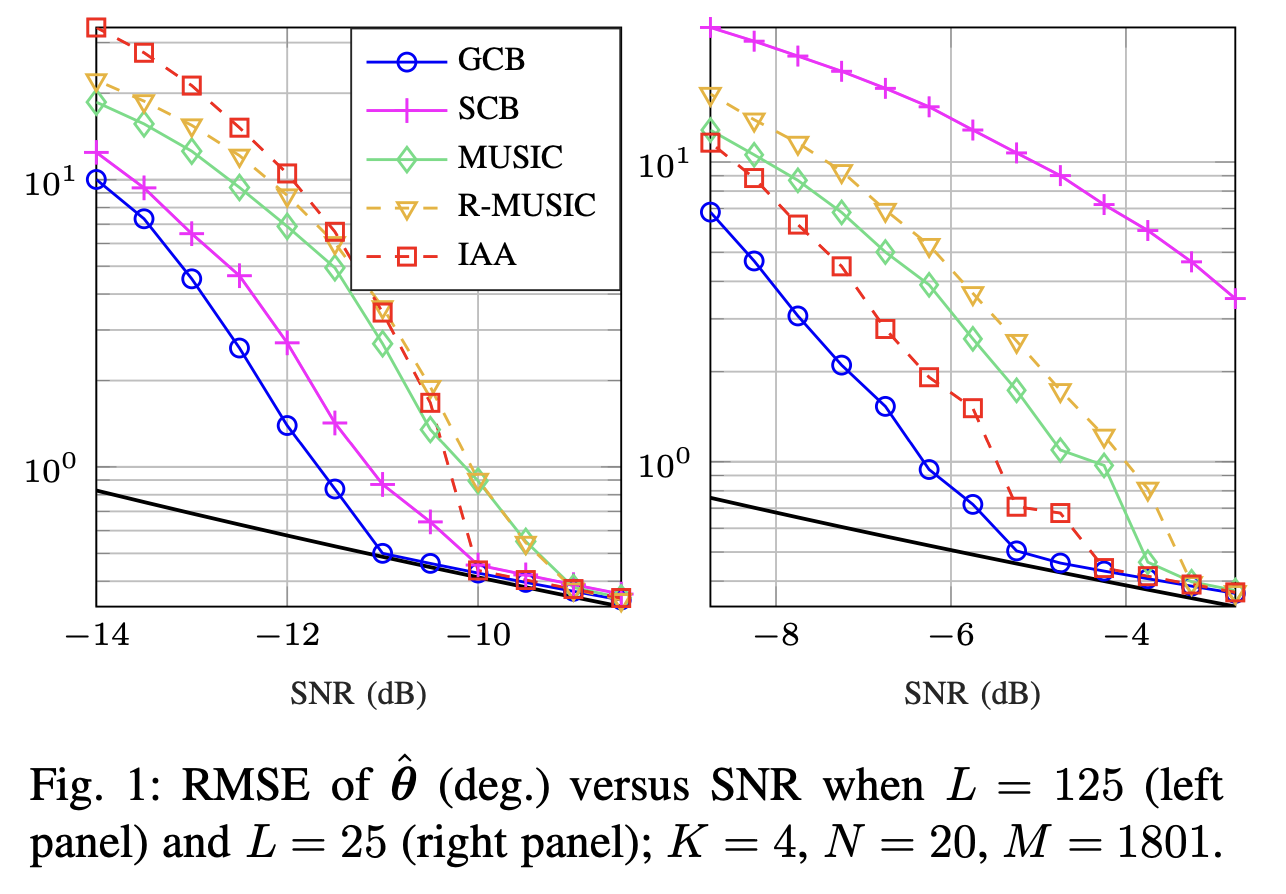For more information, see:
Greedy Capon Beamformer, Esa Ollila arXiv:2404.15329 [eess.SP], Apr. 7, 2024.
[Github]
Covariance Learning Orthogonal Matching Pursuit (CL-OMP)
Code (both MATLAB and python functions) for the Covariance Learning Orthogonal Matching Pursuit (CL-OMP) method. Also a demo simulation that reproduces Figure 1 in the paper is provided.
Comparison in the simulation study is also made to SOMP, and a function to compute it is also provided.
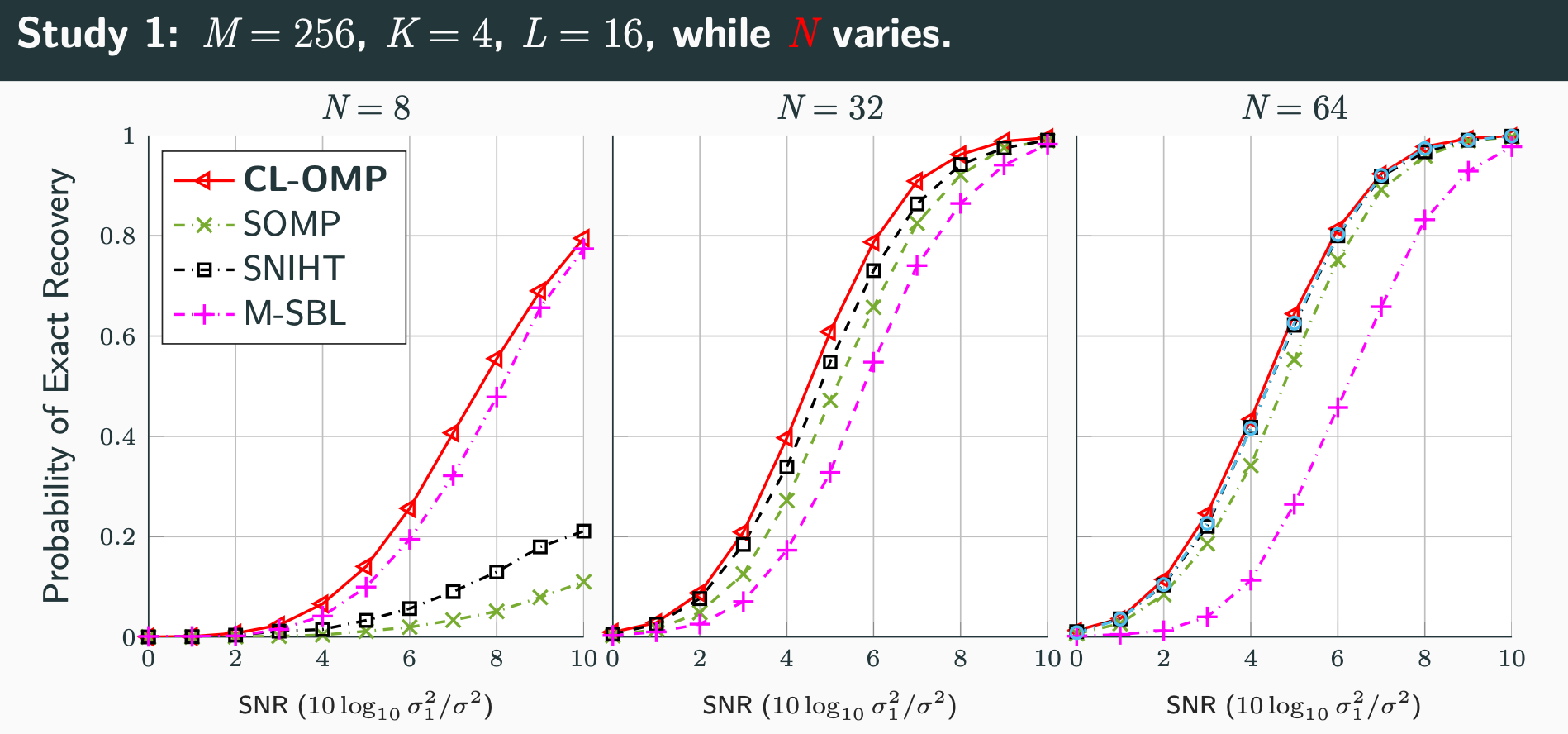For more information, see:
Matching Pursuit Covariance Learning, Esa Ollila Proc. 32nd European Signal Processing Conference (EUSIPCO'24), Lyon, August 26-30, 2024, pp. 2447-2451.
[Github] [PDF] [Slides]
Regularized tapered sample covariance matrix
Tabasco toolbox provfilides an easy to use function for computing the TABASCO (TApered or BAnded Shrinkage COvariance) estimator.
Tabasco is a covariance matrix estimation method that combines tapering or banding of the sample covariance matrix with shrinkage towards scaled identity matrix. It enjoyes benefits of both approaches:
tapering/banding leverages on the assumed structure of the covariance matrix while optimal shrinkage guarantees that the obtained ovariance matrix estimator is positive definite,
while still preserving the structure applied using banding or tapering template. Optimal parameters, e.g., the bandwidth of banding matrix, or the shinkage intensity coefficient minimizing the MSE
are adaptively estimated from the data. We also include a demo example that reproduces Figure 2 (upper left corner plot) in our paper.
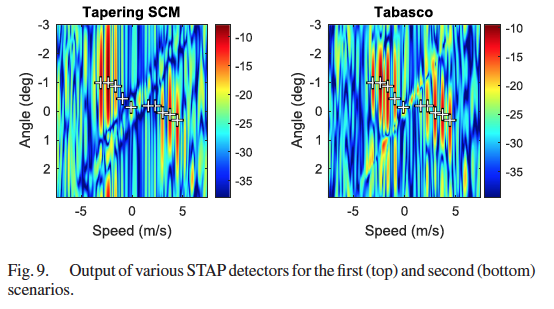For more information, see:
Regularized Tapered Sample Covariance Matrix, Esa Ollila and Arnaud Breloy, IEEE Transactions on Signal Processing, vol. 70, pp. 2306-2320, 2022.
[Matlab toolbox]
Linear pooling of sample covariance matrices
Linpool toolbox provides an easy to use function for computing an estimator of the population covariance matrix in the setting where there are data from K populations available.
We propose estimating each class covariance matrix as a distinct linear combination of all class sample covariance matrices. This approach is shown to reduce the estimation error when the sample sizes are limited, and the true class covariance matrices share a somewhat similar structure.
We provide an effective data adaptive method for computing the optimal coefficients in the linear combination that minimize the mean squared error under the general assumption that the samples are drawn from (unspecified) elliptically symmetric distributions.
An application in global minimum variance portfolio optimization using real stock data is also given.
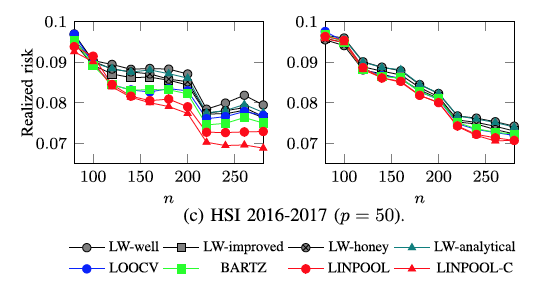For more information, see:
Linear Pooling of Sample Covariance Matrices, Elias Raninen, David E. Tyler, and Esa Ollila,IEEE Transactions on Signal Processing, vol. 70, pp. 659-672, 2022.
[Matlab toolbox]
[ Slides]
[youtube video]
Coupled regularized sample covariance matrix estimator for multiple classes
CoupledRSCM toolbox for Matlab/R/python provides an easy to use function for computing regularized SCM (RSCM) estimators for multiclass problems that couple together two different target matrices for regularization: the pooled (average) SCM of the classes and the scaled identity matrix.
Regularization toward the pooled SCM is beneficial when the population covariances are similar, whereas regularization toward the identity matrix guarantees that the estimators are positive definite. We derive the MSE optimal tuning parameters for the estimators as well as propose a method for their estimation, avoiding commonly used computer intensive cross-validation.
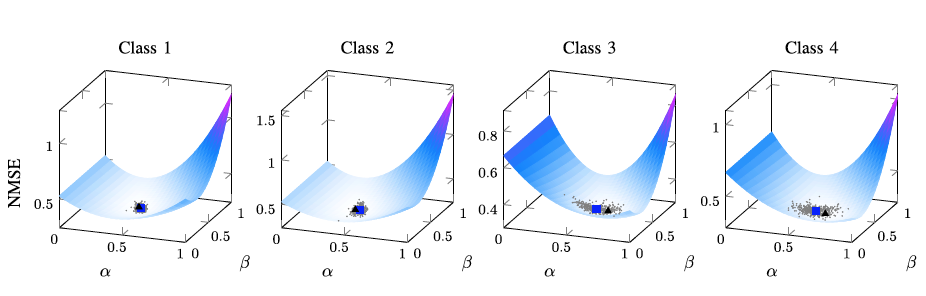For more information, see:
Coupled Regularized Sample Covariance Matrix
Estimator for Multiple Classes, Elias Raninen, David E. Tyler, and Esa Ollila,IEEE Transactions on Signal Processing, vol. 69, pp. 5681-5692, 2021
[toolbox]
Bias adjusted sign covariance matrix
BASIC toolbox for Matlab provides an easy to use function for computing
the BASIC (Bias Adjusted SIgn Covariance) estimator as well as BASIC
Shrinkage estimator (BASICS), which is better suited for high
dimensional problems, where the dimension can be larger than the sample
size. It is well-known that the widely popular spatial sign covariance matrix (SSCM)
does not provide consistent estimates of the eigenvalues of the shape matrix (trace normalized covariance matrix).
BASIC alleviates this problem by performing an approximate bias correction to the eigenvalues of the SSCM.
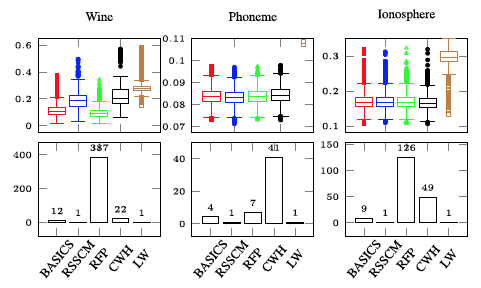For more information, see:
Bias adjusted sign covariance matrix, Elias Raninen and Esa Ollila,IEEE Signal Processing Letters, vol. 28, pp. 2092-2096, 2021.
[toolbox]
Shrinking the eigenvalues of M-estimators of covariance
shrinkM MATLAB toolbox is a collection of functions to compute an
M-estimator of scatter (covariance) matrix whose eigenvalues are shrinked
optimally towards the grand mean of the eigenvalues. Optimality means that
the shrinkage parameter is chosen to minimize the mean squared error
data-adaptively without computationally prohibitive cross-validation
procedure. The aforementioned shrinkage (or regularized) M-estimators of
covariance are described in detail in reference below. We also include a
demo example of using these covariance matrix estimators on
simulated data.
As can be noted, the proposed robust shrinkage M-estimators
(RMVT and RHub) outperform conventional non-robust estimators
with a large margin when data is non-Gaussian:
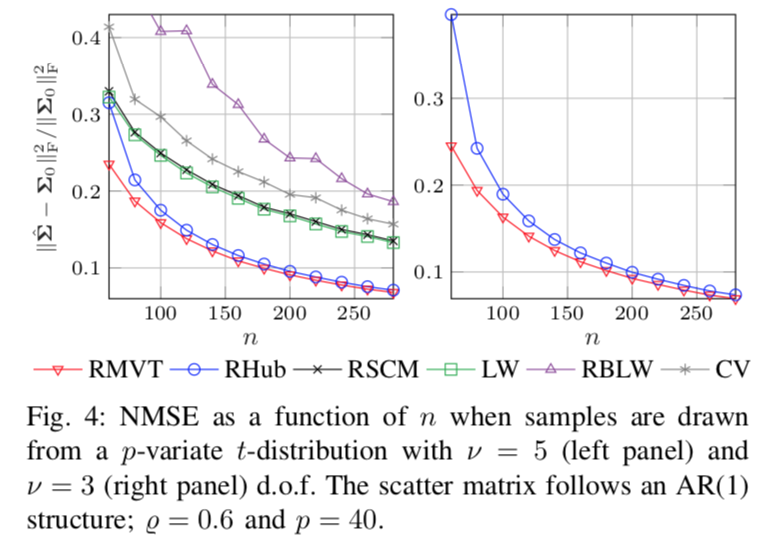For more information, see
Shrinking the
eigenvalues of M-estimators of covariance matrix, Esa Ollila, Daniel P. Palomar and
Frederic Pascal, IEEE Transactions on Signal Processing, vol. 69, pp. 256-269, 2021.
[Matlab toolbox]
[ Slides]
[youtube video]
Pedestrian detection using Riemannian classification algorithms
We have developed a python toolbox for pedestrian detection from images using classification algorithms that utilize Riemannian geometry.
For more information, see
A Comparative Study of Supervised Learning Algorithms for Symmetric Positive Definite Features, Ammar Mian, Elias Raninen and Esa Ollila,
Proc. European Signal Processing Conference (EUSIPCO'20), Amsterdam, Netherlands, August 24-28, pp. 950-954. 2020.
[
Python toolbox]
[pdf]
Block-wise Minimization-Majorization algorithm for Huber's criterion
Huber's criterion can be used for robust joint estimation of regression and scale parameters in the linear model.
The codes use the block-wise minimization majorization framework with novel data-adaptive
step sizes proposed in our paper for both the location and scale. Sparse signal
recovery using Huber's criterion can be performed using the normalized iterative
hard thresholding approach which is also implemented in the toolbox. We
illustrate the usefulness of the algorithms, hubreg and hubniht
in an image denoising application and simulation studies. For image denoising,
we provide an easy-to-use function hubniht_denoising. An example of HUBNIHT denoising
performance of Lena image in salt-and-peper noise is shown below:
and the Matlab script that produced the results is shown here.
For more information about the method, see
Block-wise minimization-majorization algorithm for Huber's criterion:
sparse learning and applications by Esa Ollila and Ammar Mian, in
Proc. IEEE International Workshop on Machine Learning for Signal Processing (MLSP'20),
Sep 21-24, 2020, Espoo, Finland, pp. 1-6.
[Toolbox]
[Slides]
Compressive Regularized Discriminant Analysis
CompressiveRDA MATLAB toolbox contains function to compute the CRDA classifiers
introduced in the reference below. The proposed classifiers can be applied in
high-dimensional sparse data scenarios, where the sample size is smaller than
the dimension of the data, which is potentially very large. Our method is especially designed for feature selection purposes and can be used as a gene selection method in genomic studies. The toolbox also contains demo examples of classification
of real-world data sets used in our paper.
One reason for success of CRDA can be its ability to find patterns in data as
shown in this gene heat map:
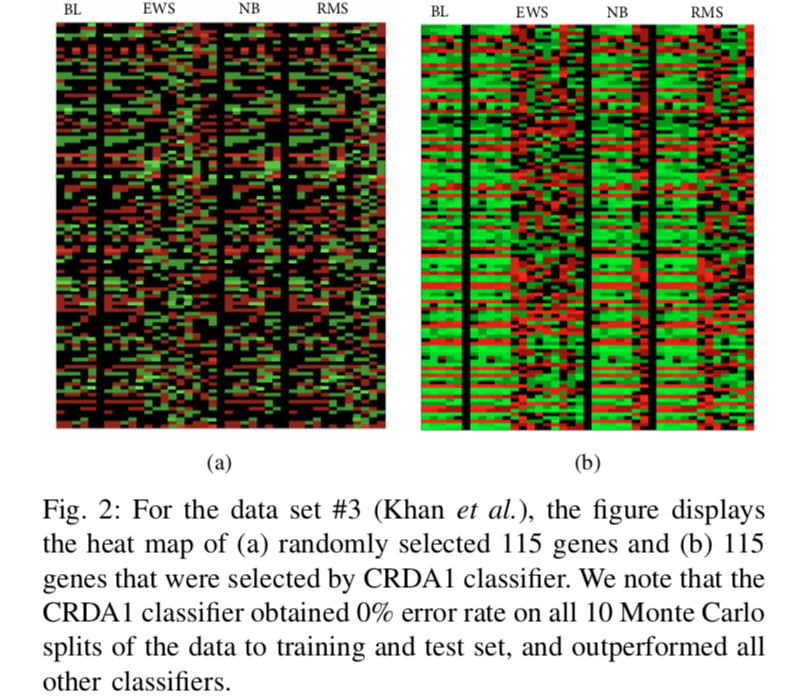For more information, see
A Compressive Classification Framework for High-Dimensional Data,
Muhammad N. Tabassum and Esa Ollila, IEEE Open Journal of Signal Processing, Vol 1., pp. 177-186, 2020.
[Matlab toolbox]
Regularized Sample Covariance Matrix (RSCM) Estimator
RegularizedSCM MATLAB toolbox contains function to compute the Ell-RSCM estimators of the
covariance matrix introduced in the reference below. The proposed estimators can be applied in
high-dimensional sparse data scenarios, where the sample size is smaller than
the dimension of the data, which is potentially very large.
The toolbox also contains demo examples arising from finance and classification.
In the former, the estimators are applied in portfolio
optimization problem of real data, where we use historical (daily) stock
returns from the Hong Kong's Hang Seng Index (HSI) and
Standard and Poor's 500 (S&P 500) index. In the latter, the estimators are used
in classification problem of real data sets using the framework of regularized
discriminant analysis. In both cases, the proposed estimators are able to yield better
performance than the state-of-the-art methods. See example below:
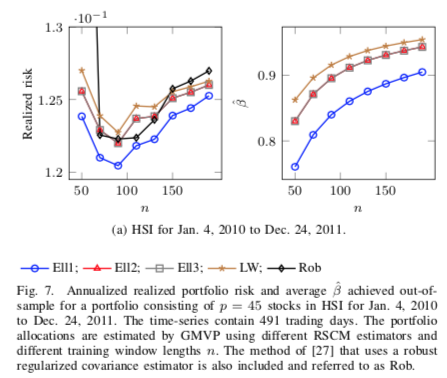For more information, see
Optimal shrinkage covariance
matrix estimation under random sampling from elliptical distributions,
Esa Ollila and Elias Raninen, IEEE Transactions on Signal Processing, vol. 67, no. 10, pp. 2707 - 2719, 2019.
[Matlab toolbox]
[ Slides]
[youtube video]
Novel FastICA power iteration algorithm
This MATLAB toolbox contains function to compute the fastICA power iteration estimator,
called PowerICA, that was proposed in the reference below. PowerICA method is efficient
alternative to conventional FastICA estimator in the cases when the sample size is not orders
of magnitude larger than the data dimensionality. This is the finite-sample regime in which
the (fixed-point) FastICA algorithm is often reported to have convergence problems. The
estimator is thus useful in many real data problems where FastICA is commonly used
such as blind-source separation of fMRI data. This is illustrated in the simulation example below:
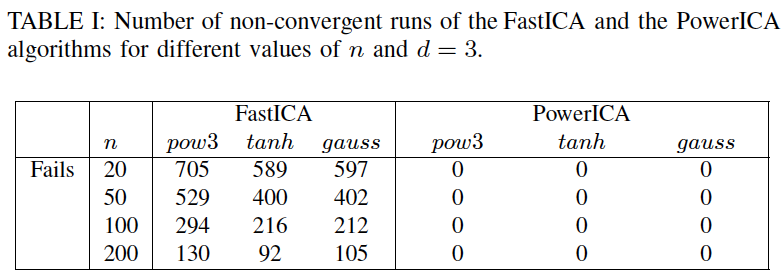For more information, see
Alternative derivation of FastICA with novel power iteration algorithm,
Shahab Basiri, Esa Ollila and Visa Koivunen, IEEE Signal Processing Letters, vol. 24, no 9, 2017.
[Matlab toolbox]
Reliable and fast bootstrap-based inference in the ICA model
This software contains function to compute the low complexity and stable bootstrap procedure
for FastICA estimators, referred to as enhanced fast and robust bootstrap (EFRB) method
for FastICA, which was introduced in the reference below.
Our bootstrapping techniques allow for performing cost efficient and reliable
bootstrap-based statistical inference in the ICA model. Performing statistical
inference is needed to quantitatively assess the quality of the estimators and
testing hypotheses on mixing coefficients in the ICA model. EFRB is shown to provice
accurate description of the distribution of FastICA mixing matrix estimator:
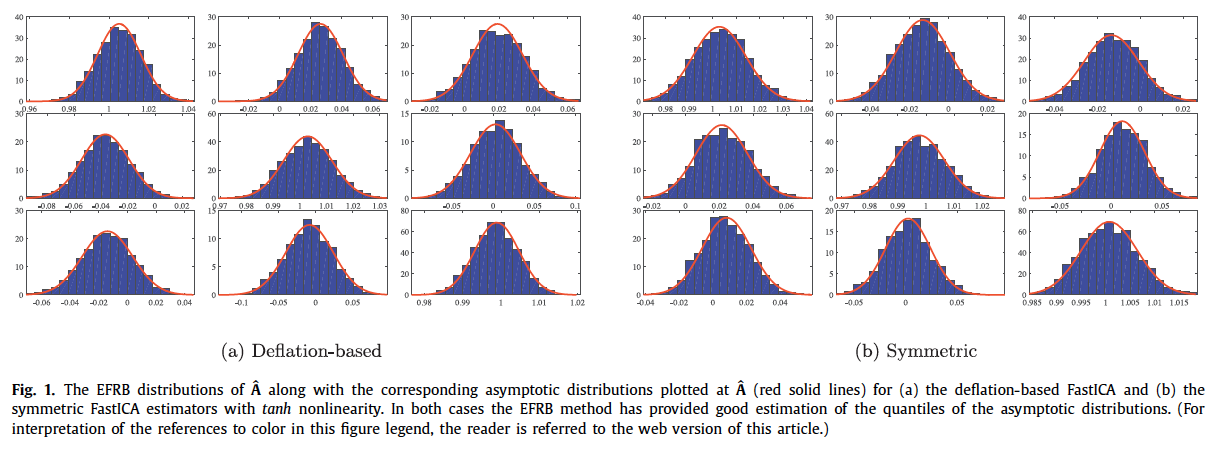For more information, see
Enhanced bootstrap method for statistical inference in the ICA model
Shahab Basiri, Esa Ollila and Visa Koivunen, Signal Processing, vol. 138, pp. 53-62, 2017
[Matlab code]
Sparse signal recovery in the multiple measurements vector model
Download the MATLAB function that computes the HUB-SNIHT estimator introduced in the reference below.
The estimator solves the multichannel sparse recovery problem of complex-valued measurements
where the objective is to find good recovery of jointly sparse unknown signal vectors from
the given multiple measurement vectors which are different linear combinations of the same
known elementary basis vectors or dictionary.
For more information, see
Multichannel sparse recovery of complex-valued signals using Huber's criterion
Esa Ollila, in Proc. Int'l Workshop on Compressed Sensing Theory and its Applications to Radar, Sonar and Remote Sensing (CoSeRa'15), Pisa, Italy, June 16-19, 2015, pp. 32-36.
[Matlab code]
Tests of circularity
Software to compute the tests of circularity introduced in Adjusting the generalized likelihood
ratio test of circularity robust to non-normality, Esa Ollila and Visa Koivunen,
in Proc. 10th IEEE Int.'l Workshop on Signal Processing Advances in Wireless Communications
(SPAWC'09), Perugia, Italy, June 21-24, 2009, pp. 558 - 562.
[Matlab code]
Also includes code for GLRT of circularity introduced in Generalized complex elliptical distributions
Tools for (non-circular) complex elliptically symmetric distributions
This software package contains a collection of tools for random number generation from
complex elliptically symmetric (CES) distributions (including
complex normal (Gaussian), complex t-, complex generalized Gaussian, (isotropic) symmetric alpha-stable distribution)
and Wald's type circularity test.
For more information, see
Complex elliptically symmetric random
variables - generation, characterization and circularity tests,
Esa Ollila, Jan Eriksson and Visa Koivunen, IEEE Transactions on signal processing, vol. 59, no.1, pp. 58-69, 2011.
[Matlab code]
Robust regression based on Oja ranks
Software to compute the regression coefficent estimates based on Oja ranks introduced in
Estimates of regression coefficients based on lift rank covariance matrix,
Esa Ollila, Hannu Oja and Visa Koivunen, Journal of the American Statistical Association, vol. 98, no. 461, pp. 90-98, 2003.
[C code and R code]