The MATLAB® toolbox shrinkM is a collection of functions to compute an M-estimator of scatter (covariance) matrix whose eigenvalues are shrinked optimally towards the grand mean of the eigenvalues. Optimality means that the shrinkage parameter is chosen to minimize the mean squared error data-adaptively without computationally prohibitive cross-validation procedure. The aforementioned shrinkage (or regularized) M-estimators of covariance are described in detail in reference [1].

We also include a demo example of using these covariance matrix estimators on simulated data. In the demo example, the data is generated from a Gaussian distribution with an AR(1) covariance structure. By running the demo example you can thus reproduce the figures in reference [1] related to this simulation design.

Contents

Compatibility

The code is tested on MATLAB R2019b, but should work on other versions of Matlab with no or little changes as well as all platforms (Windows 64-bit, Linux 64-bit, or Mac 64-bit).

Dependency

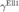this toolbox depends on RegularizedSCM toolbox; specifically, it uses its ellkurt and gamell1 functions, which compute the elliptical kurtosis parameter $\kappa$ and the (Ell1-)sphericity measure $\gamma^{\mathrm{Ell1}}$, respectively.

Hence, please install the RegularizedSCM toolbox before installing the toolbox. It is simple: just download this file and double click it in order to allow MATLAB® to install the toolbox correctly to your path.

Installation for MATLAB version >= 2014b

Download the MATLAB toolbox installation file shrinkM.mltbx. Double click the downloaded file and the MATLAB® installs the toolbox. If it does not work follow the instructions below for installation for MATLAB version < 2014b.

Installation for MATLAB version < 2014b

  1. Extract the ZIP File shrinkM.zip to a local folder. It creates shrinkM directory to your local path.
  2. Add the shrinkM folder to the MATLAB search path as follows. Start MATLAB and go to the shrinkM folder, and execute the lines:
addpath(pwd) %<-- Add the toolbox to the MATLAB path
save path  %<-- Save the path %

How to cite

If you use this toolbox or any of its function, please cite the the publication:

Now you are good to go!

Getting started

To get help of individual functions, type help followed by the function name in MATLAB command window, e.g., to get help on RSCM function, type:

help RSCM

% You can do the same for other functions such as for |RMVT|, |RHub|, |RTyl| for
% example.

  RSCM computes regularized (shrinkage) sample covariance matrix (SCM) 
  using  shrinkage estimator proposed in [1]. The function computers either 
  RSCM-Ell1 or RSCM-CV estimator.   
 
  The Data is assumed to be centered (or symmetry center parameter = 0). 
                
  INPUT 
  -----
    X       : the data matrix with n rows (observations) and p columns.
              observations can be real or complex-valued. 
 
  Name-Value Pair Arguments
  -------------------------
  RSCM can be called with numerous optional arguments. Optional
  arguments are given in parameter pairs, so that first argument is
  the name of the parameter and the next argument is the value for
  that parameter. Optional parameter pairs can be given in any order.
 
  Name      Value and description
 ==========================================================================
  --Basic parameter is the choise of the estimator to use
 
  'approach' : (string) defines which method is used to estimate the 
        shrinkage parameter beta. Valid choises are 
            'ell1' (default)    use RSCM-ELL1 estimator
            'cv'                use RSCM-CV (uses cross validation)
 ==========================================================================
 
   Optional inputs if 'approach' is 'ell1': 
  
  'kappa' : real number > -2/(p+2).
        corresponds to elliptical kurtosis parameter to use. Must
        be larger than kappa_lowerb = -2/(p+2). If not given, the the
        function estimates kappa using the marginal kurtosis values. 
 
  'gamma' : real number between [1,p] 
        Sphericity measure to use.  By default, the function 
        computes the Ell1-estimator of sphericity. 
 
 ==========================================================================
   
   Optional inputs if approach selected was 'cv': 
 
  'CV'    : positive integer (default = 5)
        when CV is positive integer K, then K-fold cross-validation is used 
 
  'betas' : nonnegative vector with elements in [0,1]
        specifies the grid of beta valuues. If not given, then default grid 
        is beta=0:0.025:1
  
 ==========================================================================
 
  OUTPUT
  ------
    Sest    : The shrinkage SCM equal to beta0*S + (1-beta0)*[Trace(S)/p]*I
    beta0   : the found optimal MMSE/CV shrinkage parameter beta
    S       : the SCM
    stats   : a structure array with fields
        .eta     : trace(S)/p 
      if 'approach'='ell1' then also fields
        .kapest  : elliptical kurtosis kappa 
        .gamest  : Ell1-estimate of sphericity
      if 'approach'='cv' then also fields
        .CV      : value K used for K-fold cross-validation
        .betas   : grid of beta values used in cross-validation
 
  REFERENCE 
  ---------
   [1] E. Ollila, D.P. Palomar, and F. Pascal, "M-estimators of scatter with 
                    eigenvalue shrinkage", Arxiv, 2020. 
 
  Author: Esa Ollila, May 2020, Aalto University. 
 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

to have a quick acces to the provided demo example in the toolbox simply type

demo shrinkM

Contact

Esa Ollila Research group website
esa.ollila@aalto.fi Toolbox website


Published with MATLAB® R2019b