The MATLAB toolbox CompressiveRDA is a collection of Matlab functions that can be used to compute Compressive Regularized Discriminant Analysis (CRDA) classifiers proposed by Tabassum and Ollila (2019).
We include a demo example of using CRDA on a real data sets. Namely on data set #1 (Isolet vowels) and data set #3 (genomic data set of Khan et al.) which allows you to reproduce the results that were reported in Table 1 of the aforementioned paper.
Contents
Compatibility
The code is tested on Matlab R2018b, but should work on other versions of Matlab with no or little changes as well as all platforms (Windows 64-bit, Linux 64-bit, or Mac 64-bit).
Dependency
CompressiveRDA toolbox uses the RegularizedSCM toolbox. Please install the RegularizedSCM before installing the CompressiveRDA toolbox.
Installation for Matlab version >= 2014b
Download the Matlab toolbox installation file CompressiveRDA.mltbx. Double click the downloaded file and the Matlab installs the toolbbox. If it does not work follow the instructions below for installation for Matlab version < 2014b.
Installation for Matlab version < 2014b
- Extract the ZIP File CompressiveRDA.zip to a local folder. It creates CompressiveRDA directory to your local path.
- Add the CompressiveRDA folder to the Matlab search path as follows. Start Matlab and go to the CompressiveRDA folder, and execute the lines:
addpath(pwd) %<-- Add the toolbox to the Matlab path save path %<-- Save the path %
How to cite
If you use this toolbox or any of its function, please cite the publication:
- Muhammad N. Tabassum and Esa Ollila, "A Compressive Classification Framework for High-Dimensional Data," Submitted for publication, arXiv:2005.04383 [stat.ML].
Now you are good to go!
Getting started
To get help of individual functions, type help followed by the function name in Matlab command window, e.g., to get help on crda function, type:
help CRDA
CRDA performs compressive regularized (linear) discriminant analysis,
referred to as CRDA, proposed in Tabassum and Ollila (2019) (see also
Tabassum and Ollila (2018) for preliminary results).
CRDA classifies each column of the test data set Xt (p x N) into one of
the G classes. Test data set Xt and training data set X must have the
same number of rows (features or variables). Vector y is a
class variable of training data. Its unique values define classes; each
element defines the class to which the corresponding column of X belongs.
The input y is a numeric vector with integer elements ranging from
1,2,..,G, where G is the number of classes. Note that y must have the
same number of rows as there are columns in X. The output yhat indicates
the class to which each column of Xt has been assigned. Also yhat is Nx1
vector of integers ranging from 1,2,...,G.
By default, the CRDA function uses the CRDA2 method which uses the Ell2-RSCM
estimator as the estimator of the covariance matrix, and cross validation (CV)
to select the optimal joint sparsity level K and the hard-thresholding
selector function.
The grid of sparsity levels K used in the range [1,p] is determined
automatically if not given as optional parameter.
For more details, we refer to Ollila and Tabassum (2019).
USAGE:
------
yhat = CRDA(Xt,X,y)
rng(iter); % for reproducibility
yhat = CRDA(Xt,X,y,Name,Value)
[yhat,B,I,k,cvstats,covstats] = CRDA(___)
EXAMPLES
--------
To call CRDA2 method you can use all of the following examples:
mc = 0;
rng(mc); % for reproducibility (due to randomness of cross validation)
yhat1 = CRDA(Xt,X,y,'verbose','on');
rng(mc); % for reproducibility (due to randomness of cross validation)
yhat2 = CRDA(Xt,X,y,'method','crda2','verbose','on');
rng(mc); % for reproducibility (due to randomness of cross validation)
yhat3 = CRDA(Xt,X,y,'q','cv','cov','ell2','K','cv','verbose','on');
isequal(yhat1,yhat2,yhat3)
Name-Value Pair Arguments
-------------------------
CRDA can be called with numerous optional arguments. Optional
arguments are given in parameter pairs, so that first argument is
the name of the parameter and the next argument is the value for
that parameter. Optional parameter pairs can be given in any order.
Name Value and description
==========================================================================
'cov' is specifies which covariance matrix estimator is to be
used in the LDA discriminant rule. Two state-of-the-art methods are
implemented.
'cov' (string) which estimate to use
'ell2' (default) use Ell2-RSCM estimator as detailed in
Ollila and Raninen (2019).
'ell1' use Ell1-RSCM as detailed in Ollila and
Raninen (2019)
'riemann' use Rie-PSCM estimator with Riemannian penalty
with shrinkage towards the mean of the
eigenvalues of the sample covariance matrix.
The estimator is computed using the
Newton-Raphson algorithm detailed in Tyler
and Xi (2019).
==========================================================================
'q' scalar (>=1) or string 'var' or 'inf' or 'cv'
If q is a real scalar, then it must be >= 1 and it
denotes the L_q-norm to be used in the hard
thresholding operator H_K(B,phi) in the CRDA method.
If q is equal to a string 'inf' (or 'var') then L_infty
norm will be used (or sample variance) will be used
as the hard-thresholding selector function. If q is equal to
a string 'cv', then CV is used to select the best
hard-thresholding selector function among the L_1-, L_2-,
L_inf-norm and the sample variance.
'prior' numeric vector of length G
specifies prior values used in the discriminant rule. The
elements should sum to to 1 (i.e., sum(prior)==1). Default is
uniform priors.
'kgrid' vector of integer values in the range [1,2,...p]
each element specifies a joint sparsity level K that is used in
the hard-thresholding operator H_K(B,phi). The function uses
cross-validation (CV) to pick the optimal sparsity level from
this grid. If value is not given then a uniform grid of 10
values in log-space ranging from [0.05 x p, K_ub] is used.
'nfolds' positive interger
specifies the number of folds to be used in the CV scheme of
the joint sparsity values K in the kgrid.
'coefmat' real matrix of size p x G
specifies the coefficient matrix B computed from the training
data set X. This value should be equal to B = Sigma^-1 * mu,
where Sigma is the covariance matrix estimator based on the
training dataset X and mu is the p x G matrix of sample mean
vectors. Note: coefmat is specified only if you have computed
the desired covariance matrix Sigma and the related coefficient
matrix B based on it. Default value is [] which implies that
B is computed using the Ell1-RSCM, Ell2-RSCM estimator or the
Rie-PSCM estimator depending on the value of the optional
parameter 'cov'.
'mu' real matrix of size p x G
matrix with class sample mean vectors as columns.
'verbose' string equal to 'on' or 'off' (default).
When 'on' then one prints progress of the function in
text format.
Output Arguments
----------------
yhat vector of size N x 1 of integers from 1, ..., G.
specifies the group to which each column of Xt has been
assigned
B matrix of size p X G
coefficient matrix calculated by the function (if not given by
the optional argument 'coefmat'
Ind indices of the length of the row vectors of B organized in
descending order, where the length is determined by optional
argument 'q' (if q is scalar, q >=1, then the length is
determined by L_q-norm)
K the best value in the grid (= K_CV) found using CV
cvtats struct that contains data of the CV with fields:
.nfolds # of folds used in the CV scheme
.cverr accumulated errors for each K in the grid cvstats.kgrid
.kgrid the used grid of sparsity levels
.indx indices of cverr when arranged from smallest to largest
.q0 the q-value picked by CV (1,2,Inf, or 0=sample variance9
.indxq0 index of picked q from the list qvals = [inf,0,2,1]
-------------------------------------------------------------------------
See also: CRDA0, CRDA_COEFMAT, HARD_THRESHOLD
DEPENDENCIES:
-------------
Install the toolbox regularizedSCM needed for computation of Ell2-RSCM
and Ell1-RSCM covariance matrix estimator:
http://users.spa.aalto.fi/esollila/regscm/
R-version available at:
https://github.com/mntabassm/compressiveRDA
REFERENCES:
------------
If you use this code in your research, then please cite:
[1] M.N. Tabassum and E. Ollila,"A Compressive Classification Framework
for High-Dimensional Data," preprint, submitted for publication,
Oct. 2019.
AUTHORS
-------
Esa Ollila and Muhammad Naveed Tabassum, Aalto University, October 2019.
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
to have a quick acces to the provided demo examples in the toolbox simply type
demo CompressiveRDA
Contact
 |
| 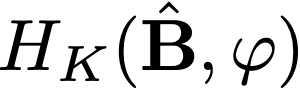 |