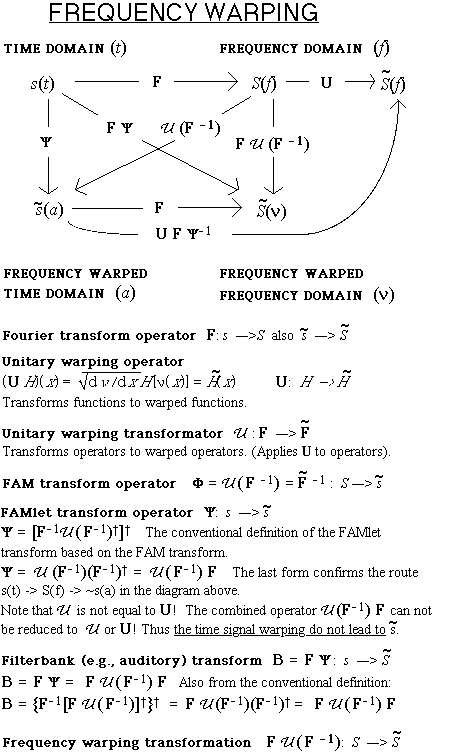
The following figure collects and organizes the basic operators and transforms related to the process of frequency warping. Some of the basic concepts are discused in the following.
This is a preliminary summary and is still open to changes partially due to the comments we are presently collecting. Therefore, if you have any comments or questions please contact the author.
The frequency warping concept is used in many ways in the literature depending on topics, contexts and authors in question.
In our studies the basic concepts of frequency warping are defined in the following way:
Frequency warping of a function H(f) is performed by applying the unitary warping operator U to the function. (The operator is defined below, refer to the figure).
Some authors have used the concept axis warping in connection to the U operator, however, the axis (f) is unchanged because the operator is a H-> ~H mapping. Instead of warping the axis the operator has created a new, unitarily warped representation ~H for the function H on the same, unchanged axis. This operation could also be called frequency mapping.
Note that the warping of a function will change its local density. Frequency warping always affects the spectral density.
An example of a frequency warped class of orthonormal functions is the FAM class. The FAM class can be seen as frequency warped complex exponentials (complex sinusoids) and the corresponding transform as the frequency warped inverse Fourier transform (S -> ~s).
Frequency warping transformation is a process where one spectral representation on a certain frequency scale (e.g., Hz, f-domain) and with a certain frequency resolution (most often uniform) is transformed to another representation on a new frequency scale (e.g., Bark or ERB-rate scale, v-domain). The new representation has a uniform frequency resolution on the new scale - however, it has a nonuniform resolution when observed from the old scale. The new frequency scale (v-domain) and the old one (f-domain) are related by a smooth and monotonic warping (mapping) function v(f) with a positive derivative (dv/df > 0).
Sometimes the term "frequency warping transformation" is shortened to frequency warping or to frequency transformation. The essential difference between the frequency warping and the frequency warping transformation is that the first one maps the information back to the same domain f -> f whereas the second transfroms it to a new domain f -> v.
Typically only band limited signals are considered. Thus both domains f and v are finite. It is practical to normalize the warping function so that the average value of the derivative dv/df is one and if no warping occurs ( v(f)=f ) the derivative equals to one everywhere. In other words, if in some frequency range the derivative is larger than one there must be another range where it is less than one.
The warping function v(f) defines how individual frequency components and different frequency ranges are mapped on the new scale. It also defines how the resoluion of the new representation is allocated, which ranges in the original representation are compressed (shrinked, resolution reduced) and which expanded (stretched, resolution increased). High values of the derivative dv/df indicate a range where the spectral representation is expanded and the resolution is increased. Correspondingly, low values of the derivative indicate the ranges of resolution reduction. At the turning frequency where dv/df=1 the spectral resolution is unchanged.
One important practical application where a warped spectral representation is required is in the computation of auditory spectra ~S(v) from audio signals s(t) or from their Fourier spectra S(f).
As indicated in the following figure there are three main ways a frequency warped spectral representation in the v-domain can be created:
The first method when combined to one operation , is equivalent to spectral domain processing with a nonuniform resolution filterbank made of warped (frequency domain) sinc functions.
Which method is chosen depends on the actual practical limitations, e.g., in the implementation of the warping process.
Some details are further discussed in the following notes.

The basic studies related to frequency warping, FAM and FAMlet classes are mainly financed by the Academy of Finland.
The author is grateful to Lic. Tech. Toomas Altosaar for his valuable comments on this text..